LEY DEL COSENO ~ Pontezuela Virtual

La ley del coseno (o teorema de los cosenos) es un resultado de trigonometría que establece la relación de proporcionalidad existente entre las longitudes de lados de un triángulo cualquiera con los cosenos de sus ángulos interiores opuestos. Este teorema es una generalización del teorema de Pitágoras (la razón de ello se encuentra en la nota del siguiente apartado).

Para aplicar el teorema del coseno se necesita conocer la longitud de dos lados y la medida de un ángulo interior

Ley del coseno

Sea un triángulo cualquiera con lados aa, bb y cc y con ángulos interiores αα, ββ y γγ (son los ángulos opuestos a los lados, respectivamente).

Entonces, se cumplen las relaciones

El teorema del coseno (con demostración). Problemas resueltos de aplicación del teorema del coseno: calcular lados, ángulos y áreas de triángulos. Problemas resueltos y explicados paso a paso. Trigonometría. Bachiller.

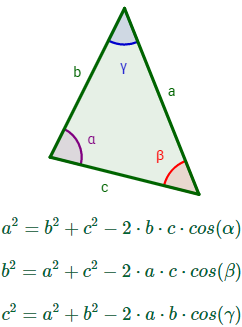
Nota: se dice que es una generalización de Pitágoras porque si uno de los ángulos es recto, el triángulo es rectángulo, siendo la hipotenusa el lado opuesto a dicho ángulo y se obtiene el teorema de Pitágoras al aplicar el del coseno.

Por ejemplo, si α = 90º, entonces, la primera de las tres fórmulas anteriores queda como

$a^{2} = b^{2} + c^{2}$

siendo a la hipotenusa del triángulo.

Problema 1

Se tiene un triángulo cuyos lados b y c miden 45 y 66 cm respectivamente y cuyo ángulo α mide 47°. Hallar cuánto mide el lado a del triángulo.

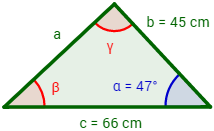
Como queremos calcular el lado a del triángulo, aplicamos la siguiente fórmula del teorema del coseno:

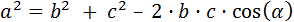
Tenemos los datos necesarios para calcular a, es decir, tenemos b, c y al ángulo α. Por tanto, sustituyendo los datos y haciendo la raíz cuadrada obtenemos:

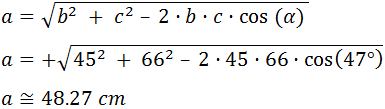
Luego el lado a mide aproximadamente 48.27 cm.

Nota: al hacer la raíz cuadrada hay que escribir el signo ±±, pero como a representa una longitud, debe ser positiva.

Nota 2: utilizamos el signo ≃≃ para indicar que el valor de a es una aproximación.

Problema 2

Si cierto triángulo tiene un lado de 25.5 cm y otro de 37.5 cm y sus respectivos ángulos opuestos son de 37° y 62°, ¿cuánto mide el otro lado?

El triángulo es el siguiente:

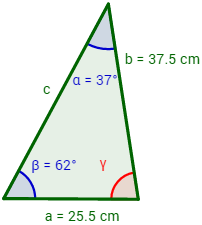
Para hallar el lado c aplicaremos la siguiente fórmula del teorema del coseno:

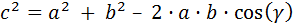
Pero para poder aplicarla, necesitamos conocer el ángulo γ. Esto no supone ningún problema ya que la suma de los ángulos interiores de un triángulo es siempre 180°, por lo que tenemos la ecuación:

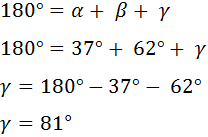
Aplicamos la fórmula:

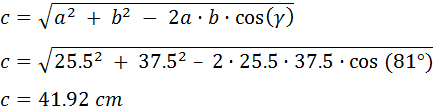
Luego el lado c mide 41.92 cm.

Problema3. Calcula los elementos de un triángulo oblicuángulo si se sabe que a = 19 cm, b = 24 cm y c = 13 cm.

Solución:

Lo primero que tenemos que hacer es recopilar nuestros datos, todo lo que el triángulo oblicuángulo nos ofrece de comienzo, para ello colocamos, los lados:

a = 19 cm.

b = 24 cm.

c = 13 cm.

Vamos a utilizar la fórmula general de la ley de cosenos, siempre y cuando hagamos los despejes correctos para llegar a las nuevas fórmulas que veremos a continuación:

$\displaystyle \cos A=\frac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$