ECUACIÓN DE LA RECTA DE LA FORMA
y= mx + b
Pero vamos por partes, ya que no existe una única versión de la ecuación de la recta, sino que de hecho hay tres formas para expresar una recta a través de una ecuación.
Ecuación general de la recta
Partiendo de uno de los postulados clásicos de la Geometría Euclidiana, señalo que para determinar una recta sólo necesitamos conocer las coordenadas de dos puntos (A y B) de un plano.
Conociendo esos dos puntos, todas las rectas de ese plano, quedan incluidas en la siguiente ecuación: ax + by + c = 0
siempre y cuando se cumplan las siguientes condiciones: a, b y c números Reales a y b no pueden ser simultáneamente nulos
siempre y cuando se cumplan las siguientes condiciones: a, b y c números Reales a y b no pueden ser simultáneamente nulos
Ecuación explícita de la recta
A esta ecuación también se le conoce con el nombre de “Ecuación punto pendiente” y ello se debe a que se trata de la ecuación de la recta que pasa solo por un punto de coordenadas conocidas y cuya pendiente también se conoce.
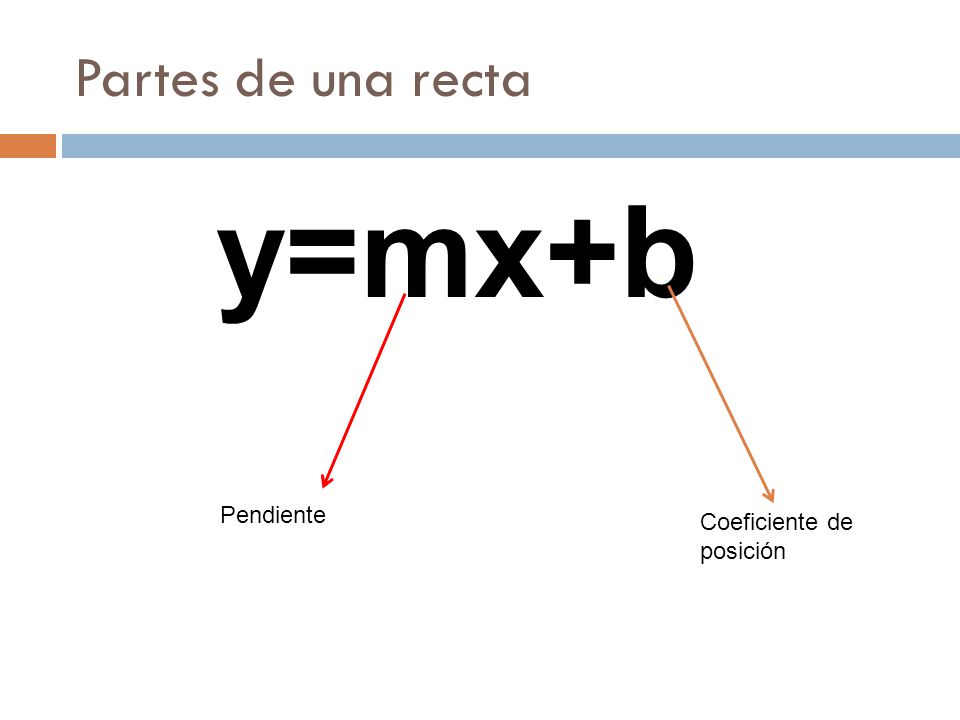
Esta es la ecuación: y = mx + b
En ella están presentes las siguientes variables:
– un punto de coordenadas conocidas (x, y)
– la pendiente (representada por m)
– la ordenada al origen (representada por n), que es el punto de corte de la recta con el eje de las ordenadas.
Ecuación de la recta que pasa por dos puntos
El fundamento teórico de esta ecuación se sustenta a partir del conocimiento de dos puntos de coordenadas conocidas y que pertenezcan a una misma recta. La expresión algebraica de la misma es la siguiente, donde los sub índices de las letras representan las coordenadas de uno y otro puntos conocidos respectivamente:
DETERMINACIÓN DE LA ECUACIÓN DE LA RECTA DE LA FORMA Y = mx +b
Después de toda esta explicación , vamos a determinar la ecuación de una recta cuando se conoce se pendiente y un punto de ella. Para ello observemos el siguiente vídeo:
Ejemplo . ¿Cuál es la ecuación de la recta que pasa por el punto (4, – 5) y su pendiente es 3?
Solución:
El único punto que tenemos es (4, -5), que lo podemos asociar a y lógicamente m = 3, dicho de otra forma:
y lógicamente m = 3, dicho de otra forma:



Si la ecuación de la recta es: 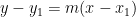
Vamos a sustituir nuestros datos, en dicha fórmula:

Simplificando

El único punto que tenemos es (4, -5), que lo podemos asociar a
Vamos a sustituir nuestros datos, en dicha fórmula:
Simplificando
cambiando de lado al 5 , tenemos :
y = 3x -12 -5
por lo tanto , la ecuación es : y = 3x -17
ACTIVIDAD
Hallar la ecuación de la recta , según su punto y pendiente :
1) P ( 6, 2 ) ; m = 5
2) P ( 3, 7 ) ; m = 4
3) P ( 8, 5 ) ; m = - 3
4) P ( 2, 1 ) ; m = 2
5) P ( 1, - 3 ) ; m = 5
6) P ( 4, 5 ) ; m = 4
7) P ( 1, 1 ) ; m = -3
8) P ( 0, - 2 ) ; m = 7
9) P ( -2, - 2 ) ; m = 2
10) P ( 7, -1 ) ; m = 3
ATENCIÓN: Transcribir la actividad al cuaderno, tomas una foto con la actividad resuelta y la envías al correo del profesor Raúl Camelo: raulc472@hotmail.com o al formulario que aparece abajo para tu evaluación.

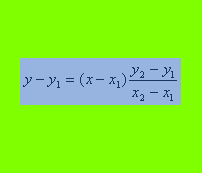

No hay comentarios:
Publicar un comentario