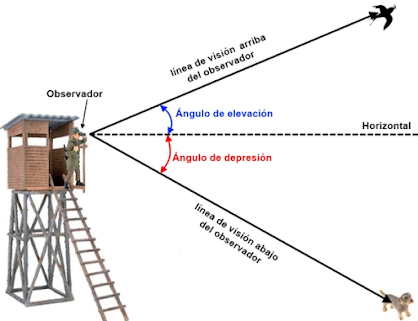
En la siguiente imagen podemos apreciar en qué consisten los ángulos de elevación y depresión:
Dentro de la vida cotidiana, los seres humanos, en su mayoría, tenemos el don de la vista, cuando observamos logramos realizar distintas posiciones hacia el horizonte, hacia lo que veamos, de ahí surgen los términos de ángulos de elevación y de depresión. Como lo observaremos en la siguiente imagen, vamos a distinguir donde se forma el ángulo de elevación y donde se forma el ángulo de depresión.
Similarmente, cuando observas un objeto abajo de tí, hay un ángulo de depresión entre el plano horizontal y tu línea de visión hacia el objeto. Observa los siguientes videos , te ayudaran a comprender el tema : Ejemplo No 1 Un piloto de un barco observa al vigía de un faro con un ángulo de elevación de 32º. Si la altura del faro es de 135 m, calcular la distancia del faro al barco, y la visual del piloto. (Una observación muy válida: si fuera el vigilante del faro el que observara al piloto del barco, entonces hablaríamos de angulo de depresión) Solución. Observemos la figura.  Se ha generado un triangulo rectángulo, recto en la base del faro. La visual del piloto es la hipotenusa, el ángulo de elevación está formado con la hipotenusa y la horizontal, Luego podemos construir un triangulo auxiliar donde ubicaremos a información suministrada, o si lo prefiere en el mismo dibujo. 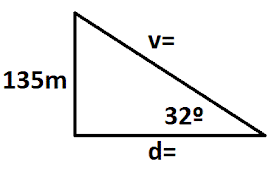 Hallamos d con la función tangente, ya que conocemos el cateto opuesto al ángulo de 32º y vamos a buscar el cateto adyacente  Ahora calculamos la visual v (hipotenusa) con la función Seno de 32º  Ambos resultados, al trabajarlos directamente en la calculadora científica, ofrecen un poco de diferencia en los decimales. Ejemplo 2. Un electricista subido en un poste, observa a su ayudante que está en el piso a 25 metros del pie del poste, con un ángulo de depresión de 40º. Calcular la altura del poste. Solución. Nótese cómo se elabora la gráfica cuando se trata de ángulo de depresión, el cual aparece fuera del triángulo que que se genera, pero es igual al otro ángulo alterno interno La información se muestra en la gráfica. 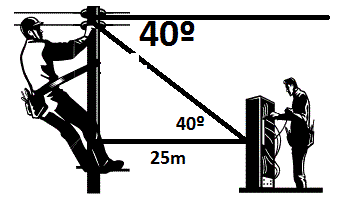 Observemos que el ángulo de depresión se trasladó al interior del triangulo NOTA: Vemos así que el ángulo de elevación, siempre es igual al ángulo de depresión, y la visual es la hipotenusa. Calculamos con tangente de 40º la altura h del poste. Usted está en capacidad de hallar la medida de la visual (v), es decir, de la hipotenusa. Por favor use la función Coseno de 50º (La respuesta es 32,76 m). ACTIVIDAD Resuelve los siguientes problemas de aplicación , utilizando las razones trigonométricas y teniendo en cuenta los ángulos de elevación y depresión: 1) Desde la cúspide de una torre de 30m de altura se observa, con un ángulo de depresión de 29°, un objeto ubicado en el mismo plano horizontal de la base de la torre. ¿A qué distancia aproximada se encuentra el objeto de la base de la torre? 2) Desde el suelo, Juan observa un avión en el cielo con un ángulo de elevación de 50°. Si la distancia entre el avión y Juan es de 800m, ¿Cuál es la altura aproximada en metros entre el suelo y el avión? 3) La medida del ángulo de depresión desde lo alto de una torre de
34 m
de
altura hasta un punto
K
en el suelo es de
80° . Calcule la distancia
aproximada del punto
K
a la base de la torre. 4) Un turista observa la parte más alta de un edificio de
15 m
de altura, con un
ángulo de elevación de
24° . Si realiza la observación con unos binoculares
que sostiene a
1,75 m
del suelo, calcule la distancia aproximada entre el
turista y la parte más alta del edificio. 5) Una mujer con una estatura de
1,64 m
proyecta su sombra en el suelo. Si
el ángulo de elevación que se forma desde la punta de la sombra hasta la
mujer es de
42° , entonces, calcule la longitud aproximada de la sombra.
6) Un ingeniero coloca un cable desde la parte más alta de una torre de
45 m
de altura hasta un punto
A
en el suelo. Si el ángulo de elevación que se
forma en el punto
A
es de
38° , calcule la longitud aproximada del cable.
|



No hay comentarios:
Publicar un comentario