En este apartado explicamos qué es y cómo se hace la resta algebraica de monomios (semejantes o no). También podrás ver ejemplos y, además, practicar con ejercicios resueltos paso a paso de la resta de monomios.
¿Cómo se restan los monomios?
Dos o más monomios solo se pueden restar si son monomios semejantes, es decir, si ambos monomios tienen una parte literal idéntica (mismas letras y mismos exponentes).
La resta de dos monomios semejantes es igual a otro monomio compuesto por la misma parte literal y la resta de los coeficientes de esos dos monomios.
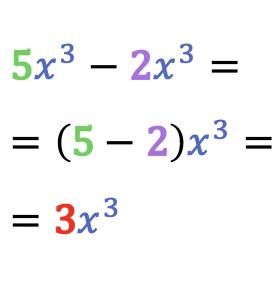
De manera que al restar un monomio menos otro monomio siempre obtendremos como resultado un monomio semejante a los dos monomios que han intervenido en la resta.
Ejemplos de restas de monomios
Te dejamos con varios ejemplos de restas entre monomios para que puedas entender del todo cómo restar dos o más monomios.
En definitiva, solo se pueden restar los monomios que son semejantes. Y, en tal caso, únicamente se restan los coeficientes, a diferencia de la parte literal que queda igual.
Por lo que respecta a las propiedades de la resta de monomios, hay que tener en cuenta que la resta no cumple con las mismas propiedades de la suma. Por ejemplo, la resta de monomios no posee ni la propiedad asociativa ni la propiedad conmutativa que sí que tiene la suma de monomios.
Puedes ver las diferencias entre estos dos tipos de operaciones en la explicación de cómo sumar monomios, donde, además, encontrarás cuáles son las propiedades de la suma de monomios junto con ejemplos y ejercicios resueltos.
A continuación se muestran diferentes ejemplos posibles en la resta de monomios:
- De 6b restar 3b. Determinando el minuendo +6b con su signo y posteriormente el sustraendo +3b con el signo de resta será:
6b – (3b) = 6b – 3b = 3b - De 18c restar 9a. Determinando el minuendo +18c con su signo y posteriormente el sustraendo +9a con el signo de resta será:
18c – (9a) = 18c – 9a En este caso no es posible simplificar ya que cada término tiene diferente letra. - De –13a2b restar 5a2b. Determinando el minuendo –13a2b con su signo y posteriormente el sustraendo +5a2b con el signo de la resta será:
–13a2 – (5a2b) = –13a2b – 5a2b = –18a2b - De –8x2y restar –4ax2. Determinando el minuendo –8x2y con su signo y posteriormente el sustraendo –4ax2 con el signo de la resta será:
–8x2y – (–4ax2) = –8x2y + 4ax2 Se recomienda que el primer término sea el positivo, por lo tanto, es posible reacomodar el resultado de la siguiente manera:4ax2 – 8x2y





No hay comentarios:
Publicar un comentario