¿Qué son los polinomios?
Antes de empezar a aprender a sumar polinomios debemos saber qué son y qué propiedades tienen. Es importante entender cuál es la parte literal, el grado y saber ordenar sus términos.
Si todavía no tienes claro estos conceptos te invito a que leas los post anteriores sobre las propiedades de los monomios y las propiedades de los polinomios.
La suma se puede hacer de dos formas distintas: en horizontal y en vertical. Vamos a ver las dos maneras y después puedes elegir cuál te resulta más fácil utilizar.
Suma de polinomios en horizontal
Para hacer las operaciones en horizontal primero escribimos un polinomio y seguido en la misma línea escribimos el otro que vamos a sumar o restar. Después, agrupamos términos semejantes.
Ejemplo:
Vamos a realizar la suma. Para ello escribimos cada uno rodeado de paréntesis y con el signo de la suma entre ellos.
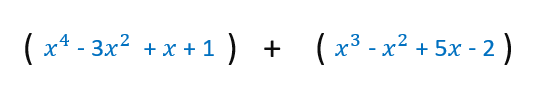
Fíjate en los términos que son semejantes entre los dos polinomios.
No podemos sumar dos términos que tienen distinto grado, solo podemos agrupar los que sean semejantes y después sumar.
En la siguiente imagen están identificados los términos semejantes rodeados con el mismo color.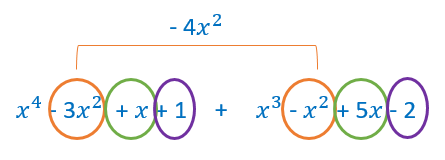
Igual que hemos hecho con el término de grado 2, debemos sumar los términos de grado 1 y los términos de grado 0.
El resultado de la suma es: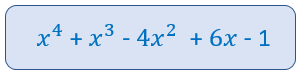
Suma de polinomios en vertical
Para hacer las sumas en vertical debemos escribir el primer polinomio ordenado. En el caso de que sea incompleto es conveniente dejar los huecos libres de los términos que falten. Después, escribimos el siguiente polinomio debajo del anterior, de manera que coincida justo debajo el término semejante al de arriba. Después, ya podemos sumar cada columna.
Ejemplo:
Vamos a ver la suma en vertical con los dos polinomios del ejemplo anterior.Fíjate en el primer polinomio. Hay que escribirlo ordenado y ver si está completo. En este caso falta el término de grado 3, entonces debemos dejar el hueco correspondiente o escribir un cero en su lugar.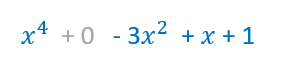
Ahora escribimos el segundo debajo del primero, de manera que coincidan los términos semejantes uno debajo de otro.
Solo queda sumar cada columna, es decir, sumar los términos semejantes.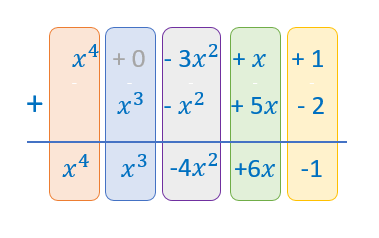
EJEMPLO
Realiza la suma de los polinomios: 
.
Solución
Podemos realizar la suma horizontalmente. Entonces, eliminamos los paréntesis y combinamos términos semejantes:
También podemos realizar esta suma verticalmente. Colocamos a cada variable con diferente exponente en su propia columna:
______________
EJEMPLO:
Realiza la suma de los polinomios: 
Solución
Nuevamente, empezamos realizando la suma horizontalmente. Para eso, necesitamos eliminar los paréntesis y combinar términos semejantes:
Ahora, podemos realizar la suma verticalmente. Separamos a las variables con diferentes exponentes en diferentes columnas y dejamos un espacio si es que un polinomio no tiene algún exponente:
________________
ACTIVIDAD
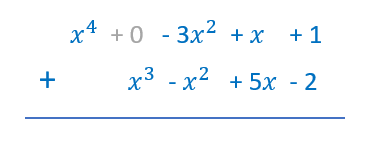
No hay comentarios:
Publicar un comentario