Experimento aleatorio
Es la reproducción controlada de un fenómeno; y cuyo resultado depende del azar. Ejemplos:
Lanzamiento de un dado.
Lanzamiento de una moneda.
Un experimento aleatorio puede ser repetido bajo las mismas condiciones, y se puede describir el número de resultados posibles.
Espacio muestral (S)
Es el conjunto de todos los resultados posibles de un experimento aleatorio.
Si se lanza un dado, el espacio muestral está compuesto por los siguientes elementos: S={1, 2, 3, 4, 5, 6}. Si se lanza una moneda que tiene dos caras: perro (P) y gato (G), el espacio muestral está compuesto por: S={P, G}.
Si se lanzan dos monedas, el espacio muestral está compuesto por: S={(P, P), (P, G), (G, P), (G, G)}.
Si se lanza un dado y una moneda, el espacio muestral está compuesto por: S={(1,P),(1,G),(2,P),(2,G),(3,P),(3,G),(4,P),(4,G),(5,P),(5,G),(6,P),(6,G)}
Evento o suceso
Conjunto de uno o más resultados del experimento aleatorio.
Si A = {obtener un número 5 al lanzar un dado}, entonces, A={5}.
Si B = {obtener un número mayor que 3 al lanzar un dado}, entonces, B={4, 5, 6}.
Si C = {obtener un número par al lanzar un dado}, entonces, C={2, 4, 6}.
Si D = {obtener al menos 1 gato al lanzar 2 monedas}, entonces, D={(P, G), (G, P), (G, G)}
La fórmula de probabilidad es la siguiente:
Mientras más se acerca el valor de la probabilidad a 0, disminuye la posibilidad de que ocurra el evento. Mientras más se acerca el valor a 1, aumenta la posibilidad de que ocurra.
0 ≤ P(A) ≤ 1 La probabilidad de que ocurra un evento es 0, si es imposible que ocurra ese evento. Por otro lado, la probabilidad de que un ocurra un evento es 1, si es seguro que ocurrirá ese evento.
Ejemplo 1: La moneda de México, tiene 2 caras: águila y sello. ¿Cuál es la probabilidad de obtener águila al lanzar una moneda?
Solución: Primero calculamos el número total de casos posibles que se dan al lanzar la moneda. En este problema, son 2 casos posibles, se obtiene águila o se obtiene sello. Ahora, calculamos el número de casos favorables. Si lanzamos la moneda, tenemos 1 caso de águila. Por lo tanto, la probabilidad de obtener águila sería:
Podemos colocar como respuesta: 0,5 o 50%.
Ejemplo 2: ¿Cuál es la probabilidad de obtener un 5 al lanzar un dado?
Solución: Primero calculamos el número total de casos posibles que se dan al lanzar un dado. En este problema, son 6 casos posibles, ya que el dado puede arrojar 1, 2, 3, 4, 5 o 6. Ahora, calculamos el número de casos favorables. Si lanzamos un dado, tenemos 1 caso en el que se obtiene 5. Por lo tanto, la probabilidad de obtener un 5 sería:
La respuesta sería: 0,1667 o 16,67%.
Ejemplo 3: Si se lanza una moneda de México al aire dos veces, ¿cuál es la probabilidad de obtener al menos 1 águila?
Solución: Primero calculamos el número total de casos posibles. Los casos posibles del primer y segundo lanzamiento son:
Águila – águila.
Águila – sello.
Sello – águila.
Sello – sello.
En total, tenemos 4 casos posibles. Ahora calculamos el número de casos en los cuáles se obtiene al menos 1 águila. Los casos son:
Águila – águila.
Águila – sello.
Sello – águila.
Es decir, tenemos 3 casos favorables. Por lo tanto, la probabilidad de obtener al menos un águila es:
La respuesta sería: 0,75 o 75%
ACTIVIDAD
Resuelve los siguientes ejercicios
1. Una moneda cuenta con 2 caras: gato y perro. ¿Cuál es la probabilidad de obtener perro al lanzar la moneda?
2.. ¿Cuál es la probabilidad de obtener un 3 al lanzar un dado?
3. ¿Cuál es la probabilidad de obtener un número menor que 5 al lanzar un dado?
4. Una caja contiene 3 bolas verdes, 5 bolas rojas y 2 bolas azules. Si se extrae una bola al azar, ¿cuál es la probabilidad de obtener una bola azul?
5. Una caja contiene 3 bolas verdes, 5 bolas rojas y 2 bolas azules. Se extraen 2 bolas al azar; si la primera bola seleccionada fue azul, ¿cuál es la probabilidad de que la segunda sea verde, dado que las bolas no reponen?
6. En una bolsa hay papelitos con los números del 1 al 10. Si se extrae un papelito al azar, calcular la probabilidad de obtener un número par.
7. Calcular la probabilidad de que, al extraer una carta de una baraja de 52 cartas, esta sea de corazones.
8. Calcular la probabilidad de que, al extraer una carta de una baraja de 52 cartas, esta sea el 5 de espadas.
9. Se lanza 2 veces una moneda, ¿cuál es la probabilidad de obtener 2 perros?
10. Calcular la probabilidad de obtener la suma 5 al lanzar dos dados.

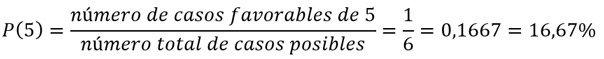
No hay comentarios:
Publicar un comentario