Aplicación del Teorema de Pitágoras

 EJEMPLOS

1)

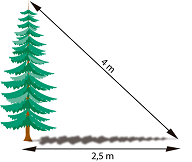
Al atardecer, un árbol proyecta una sombra de 2,5 metros de longitud. Si la distancia desde la parte más alta del árbol al extremo más alejado de la sombra es de 4 metros, ¿cuál es la altura del árbol?

Solución

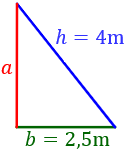
Imaginamos un triángulo rectángulo de modo que

• su base, $b$, es la sombra del árbol,

• su altura, $a$, es la altura del árbol y

• su hipotenusa, $h$, es la distancia desde el árbol al extremo de la sombra.

Como el triángulo es rectángulo, aplicamos el teorema de Pitágoras para calcular su altura, $a$:

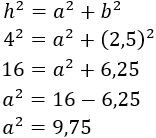
Finalmente, hacemos la raíz cuadrada:

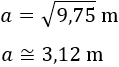
Por tanto, la altura del árbol es, aproximadamente, 3,12 metros.

 2)

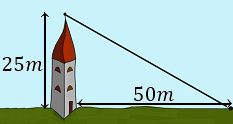
Se quiere colocar un cable desde la cima de una torre de 25 metros altura hasta un punto situado a 50 metros de la base la torre. ¿Cuánto debe medir el cable?

Solución

El cable coincide con la hipotenusa de un triángulo rectángulo cuyos catetos miden 

$a=25m$ y $b=50m$.

Calculamos la longitud del cable (es la hipotenusa $h$):

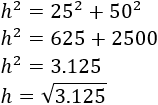
Como $3.125={25}^2\cdot 5$, podemos simplificar:

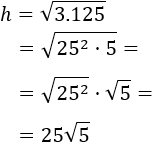
El cable debe medir $h=25\sqrt{5}$ metros, e

s decir, aproximadamente 55.9 metros.

ACTIVIDAD

Resolver los siguientes problemas:

1) Se quiere colocar un cable que parte desde la cima de la torre Eiffel (300m de altura) y que termina en el suelo a 150 metros del centro de la base de la torre:

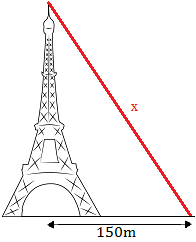
Calcular la longitud que debe tener el cable.

2) Una escalera de 15 metros se apoya en una  pared vertical, de modo que el pie de la escalera se encuentra a 9 metros de esa pared. Calcula la altura (metros), que alcanza la escalera sobre la pared.

3) Si nos situamos a 150 metros de distancia de un rascacielos, la visual al extremo superior del mismo recorre un total de 250 metros. ¿Cuál es la altura total del rascacielos?

4) Un coche que se desplaza desde el punto A hasta el punto B recorre una distancia horizontal de 35 metros, mientras se eleva una altura de 12 metros. ¿Cuál es la distancia, en metros, que separa a los puntos A y B?

5)  Un guardacostas observa un barco desde una altura de 28 metros. El barco está a una distancia horizontal del punto de observación de 45 metros. ¿Cuál es la

longitud, en metros, de la visual del guardacostas al barco?

6) Desde un acantilado de 200 metros de altura se observa un barco que se encuentra a 210 metros de dicho acantilado. ¿Qué distancia, en metros, recorre la visual desde el acantilado hasta el barco?

7) La altura de una portería de fútbol reglamentaria es de 2,4 metros y la distancia desde el punto de penalti hasta la raya de gol es de 10,8 metros. ¿Qué distancia recorre un balón que se lanza desde el punto de penalti y se estrella en el punto central del larguero?

Envía tu Actividad