TEOREMA DE PITAGORAS

 Observa el siguiente video que te demuestra el teorema

El siguiente video ye ayudara a comprender y aplicar el teorema

Teorema: dado un triángulo rectángulo de catetos a y b e hipotenusa h (el lado opuesto al ángulo recto). Entonces,

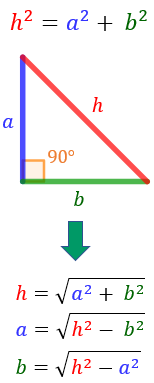
Recordemos que:

• el triángulo es rectángulo porque tiene un ángulo recto, es decir, un ángulo de 90 grados 
• la hipotenusa es el lado opuesto al ángulo recto . Es el lado de mayor longitud

Nota: h siempre es mayor que los dos catetos, es decir, h > a y h > b.

El teorema de Pitágoras es uno de los resultados más conocidos de las matemáticas y también uno de los más antiguos. Existen cientos de demostraciones de este resultado.

La pirámide de Kefrén (siglo XXVI a. C.) fue construida en base al llamado triángulo sagrado egipcio, que es el triángulo rectángulo de lados 3, 4 y 5.

La comprensión del teorema es sencilla y tiene muchas aplicaciones en la vida cotidiana, como veremos en los problemas de esta sección. Pero también tiene sus aplicaciones en las matemáticas avanzadas (análisis vectorial, análisis funcional...).

Ejemplo 1

Calcular la hipotenusa del triángulo rectángulo de lados 3cm y 4cm.

Los lados son

$$a=3cm,b=4cm$$

Aplicando el teorema de Pitágoras,

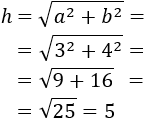
Por tanto, la hipotenusa mide 5cm.

Ejemplo 2

Si la hipotenusa de un triángulo rectángulo mide 2cm y uno de sus lados mide 1cm, ¿cuánto mide el otro lado?

Llamamos a los lados a y b y a la hipotenusa h. Sabemos que

$$h=2,a=1$$

Por Pitágoras, sabemos que

$$h^2=a^2+b^2$$

Sustituyendo los valores conocidos tenemos que

Ahora despejamos b en la ecuación

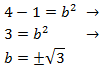
Hemos escrito los signos positivo y negativo porque es lo que, en teoría, debemos hacer. Pero como b representa la longitud de un cateto, no puede ser un número negativo.

Por tanto, el cateto mide

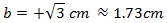
Podemos dejar la raíz cuadrada o aproximarla.

Ejemplo 3

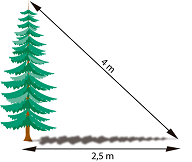
Al atardecer, un árbol proyecta una sombra de 2,5 metros de longitud. Si la distancia desde la parte más alta del árbol al extremo más alejado de la sombra es de 4 metros, ¿cuál es la altura del árbol?

Imaginamos un triángulo rectángulo de modo que

• su base, $b$, es la sombra del árbol,

• su altura, $a$, es la altura del árbol y

• su hipotenusa, $h$, es la distancia desde el árbol al extremo de la sombra.

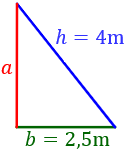
Como el triángulo es rectángulo, aplicamos el teorema de Pitágoras para calcular su altura, $a$:

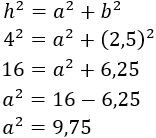
Finalmente, hacemos la raíz cuadrada:

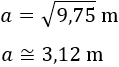
Por tanto, la altura del árbol es, aproximadamente, 3,12 metros.

ACTIVIDAD

Dibuja un triangulo rectángulo , escribe los valores indicados en cada caso y calcula el lado desconocido(hipotenusa o cateto)

1)   h=?  , a= 5 cm  , b = 12 cm

2)   h=10 cm  , a= 8 cm  , b = ?

3)   h=?  , a= 17 cm  , b = 15 cm

4)   h=?  , a= 60 cm  , b = 11 cm

5)   h=13 cm , a= 5 cm  , b = ?

6)   h= 65 cm  , a= ?  , b = 52 cm

7)   h=?  , a= 84 cm  , b = 13 cm

8)   Un faro de 16 metros de altura manda su luz a una distancia horizontal sobre el mar de           63 metros. ¿Cuál es la longitud, en metros, del haz de luz? 

       

 9)  Desde un balcón de un castillo en la playa se ve un barco a 85 metros, cuando                         realmente    se encuentra a 84 metros del castillo. ¿A qué altura se encuentra

      ese balcón?

10)    Si nos situamos a 150 metros de distancia de  un edificio, la visual al extremo   superior del mismo  recorre un total de 250 metros. ¿Cuál es la altura total    del edificio?

Envía tu Actividad