La estadística descriptiva es la rama de la estadística que recolecta, analiza y caracteriza un conjunto de datos (peso de la población, beneficios diarios de una empresa, temperatura mensual,…) con el objetivo de describir las características y comportamientos de este conjunto mediante medidas de resumen, tablas o gráficos.
Variables estadísticas
Una variable estadística es el conjunto de valores que puede tomar cierta característica de la población sobre la que se realiza el estudio estadístico y sobre la que es posible su medición. Estas variables pueden ser: la edad, el peso, las notas de un examen, los ingresos mensuales, las horas de sueño de un paciente en una semana, el precio medio del alquiler en las viviendas de un barrio de una ciudad, etc.
Las variables estadísticas se pueden clasificar por diferentes criterios. Según su medición existen dos tipos de variables:
- Cualitativa (o categórica): son las variables que pueden tomar como valores cualidades o categorías.
Ejemplos:
- Sexo (hombre, mujer)
- Salud (buena, regular, mala)
- Cuantitativas (o numérica): variables que toman valores numéricos.
Ejemplos:
- Número de casas (1, 2,…). Discreta.
- Edad (12,5; 24,3; 35;…). Continua.
Medidas de posición central
Las medidas de tendencia central (o de centralización) son medidas que tienden a localizar en qué punto se encuentra la parte central de un conjunto ordenado de datos de una variable cuantitativa.
Media
Definimos media (también llamada promedio o media aritmética) de un conjunto de datos (X1,X2,…,XN) al valor característico de una serie de datos resultado de la suma de todas las observaciones dividido por el número total de datos.
Es decir:
Visto desde un punto de vista más conceptual, la media aritmética es el centro de los datos en el sentido numérico, ya que intenta equilibrarlos por exceso y por defecto. Es decir, si sumamos todas las diferencias de los datos a la media da cero.
Mediana
La mediana (Me(X)) es el elemento de un conjunto de datos ordenados (X1,X2,…,XN) que deja a izquierda y derecha la mitad de valores.
Si el conjunto de datos no está ordenado, la mediana es el valor del conjunto tal que el 50% de los elementos son menores o iguales y el otro 50% mayores o iguales.
Moda
La moda (Mo(X)) es el valor más repetido del conjunto de datos, es decir, el valor cuya frecuencia relativa es mayor. En un conjunto puede haber más de una moda.
Ejemplo
El número de hermanos de un grupo de 5 niños es 1, 3, 0, 2 y 2.
Calculamos la media:
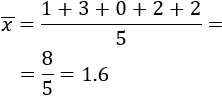
La media es 1.6 hermanos.
La moda es 2.
Ejemplo
Las alturas (en centímetros) de los 10 alumnos de una clase son 178, 163, 155, 159, 171, 155, 172, 170, 159 y 163.
Ordenamos los datos: 155, 155, 159, 159, 163, 163, 170, 171, 172 y 178.
Como hay un número par de datos, la mediana es la media de los datos de la posición 5 y 6:
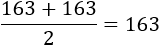
Observad que hay el mismo número de datos a uno y otro lado de la mediana (4 datos en cada lado).
Además, la media es 164.5cm y hay tres modas: 155, 159 y 163.
ACTIVIDAD
Elija el tipo de variable en cada caso:
1. El curso favorito de los alumnos de una escuela.
2. Cantidad de libros en un anaquel.
3. Diámetro de una esfera.
4. Cantidad de clientes atendidos en un restaurante en un día.
5. Lugar que ocupa un nadador en una competencia.
6. Volumen de agua dentro de una lavadora de 200 litros de capacidad máxima.
7. Longitud de 150 tornillos producidos en una fábrica.
8. Número de pétalos que tiene una flor.
9. Color de cabello de los niños que audicionan para una película de Netflix.
10. Tiempo requerido para responder las llamadas en un call center.
Hallar las medidas de tendencia central
1) Las notas del examen de matemáticas de 15 alumnos son las siguientes: 5, 3, 9, 7, 3, 6, 7, 5, 8, 7, 5, 4, 7, 6 y 8.
Calcular la media, moda y mediana de las notas.
2)La siguiente tabla proporciona el número de gatos y de perros que tienen en casa un grupo de 10 amigos:
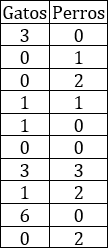
- Calcular la media, moda y mediana del número gatos.
- Lo mismo con el número de perros.
- Si sumamos el número de gatos y de perros, tenemos el número de mascotas de cada amigo. Calcular la media, moda y mediana de este dato.







No hay comentarios:
Publicar un comentario